点光源が観測者の真後ろにあるとき
陰影の作図に関するご質問があったので、その回答です。
パースフリークスでは陰影の章で詳細を説明していますので、そちらも併せてご参照ください。点光源のページでは作図例として3つの光源A,B,Cに対する影の描き方を説明しました。しかし今回のご質問は、観測者の真後ろに光源があるパターンとのことですので、新たに光源Dを置きました。
図の通りではありますが、文章で位置を定義しておきます。
- 光源は「観測者の8マス後ろかつ横位置は同じ、そして高さも同じです」(A,B,Cとは高さが違うので注意してください)
- 光源の真下の地面は「観測者の8マス後ろかつ横位置は同じ、そして高さは観測者の2マス下です」
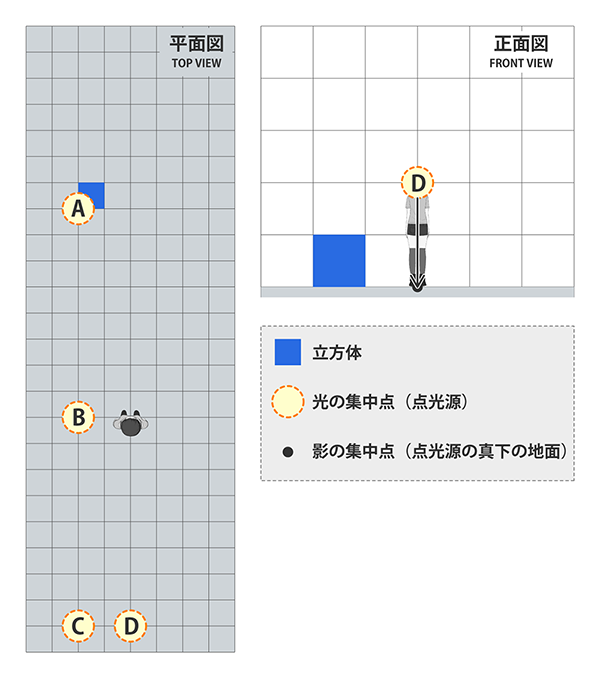
現実世界では光源を観測者の真後ろに置くと、観測者自身の影ができてしまいますが、透視図法における「観測者」は仮想の存在なので、陰影の発生には影響を与えないものとします。
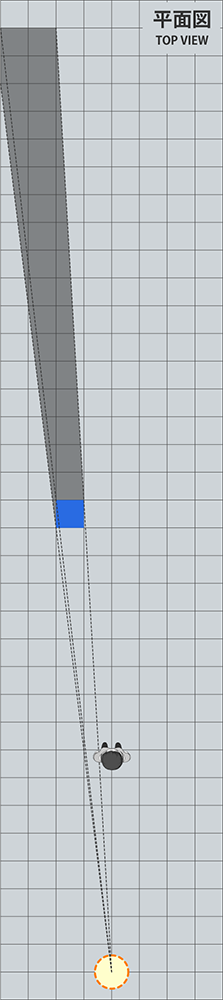
まずは簡単に平面図上で考えてみましょう。
光源から立方体に対して直線を引くことで影の位置を求めることができます。本来は平面図だけでは影がどこで終端を迎えるのかまでは分からないのですが、今回は条件が単純(光源の高さが2マス、立方体の高さが1マス)であるため、影の終わりは光源からの距離の2倍となります。
実際に3DCGで描かせてみると、上図の考えで正しいことが分かります。(1枚目は見やすいように視点を上空からにしています。2枚目は想定される観測者からの見た目です)


では、透視図法で描いてみましょう。作図上は光の集中点と影の集中点の位置さえ分かれば直線を引いて交点を求めるだけなので簡単です。
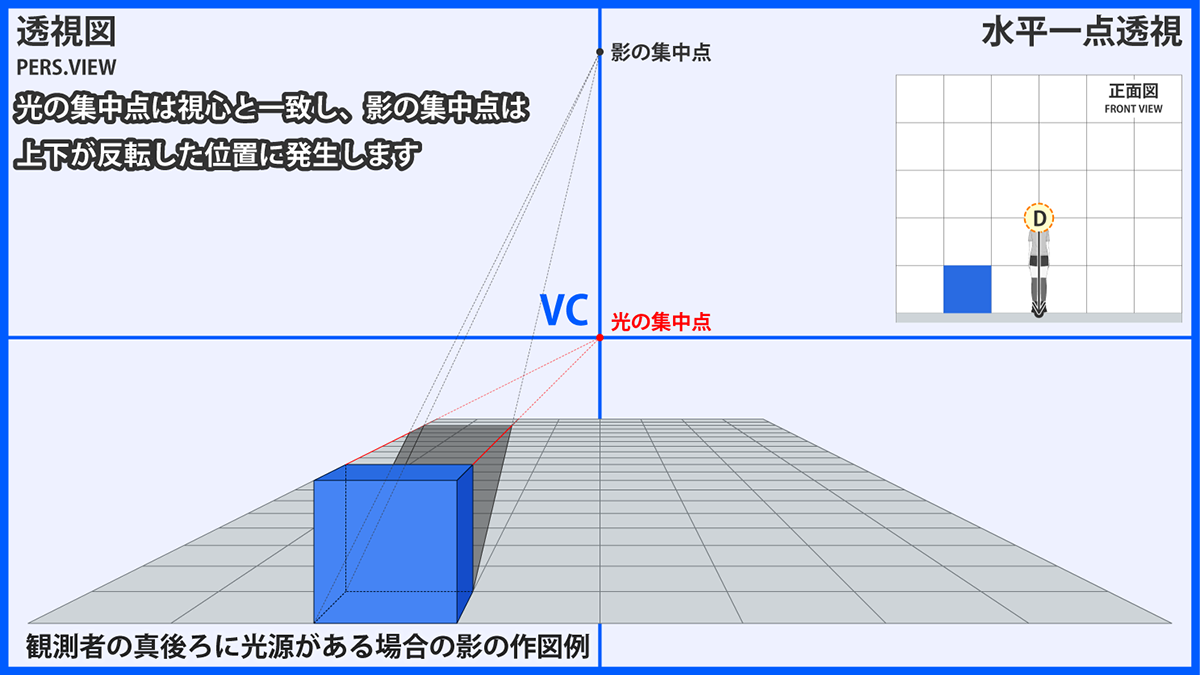
問題はその位置をどうやって求めるかですが、透視図上に平面図や側面図を重ね描きすれば、厳密な位置を割り出すことができます。ただし今回の例では光源の(平面図や正面図上での)横位置が観測者と同じであるため、集中点の位置は視心(VC)と同じ横位置に来ることが明白です。よって縦位置のみを求めれば良いことになります。
そこで平面図は省略し、側面図のみを重ね描きすることにします。
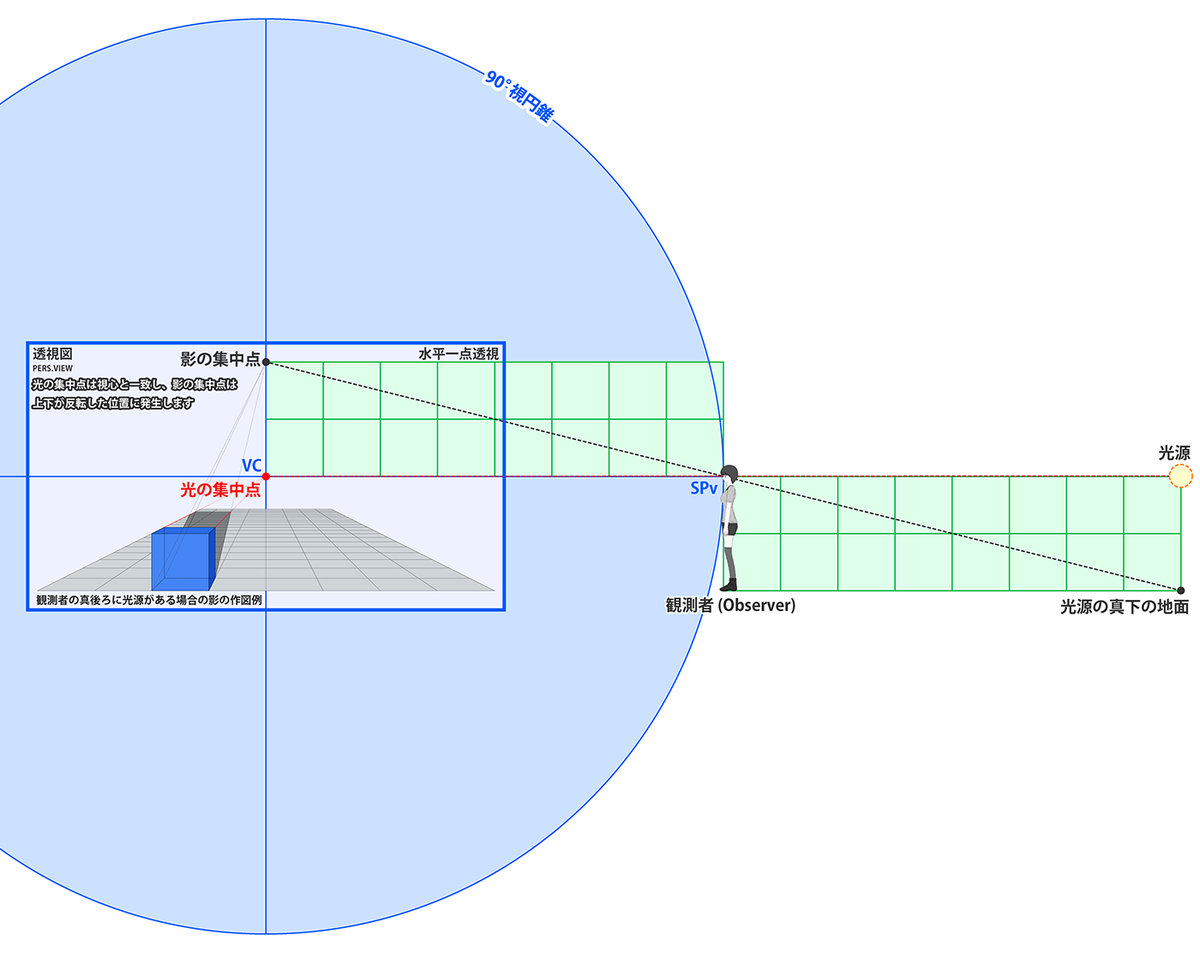
光源を観測者の8マス後ろに置き、その2マス下に光源の真下の地面を描きます。
ここから先は透視図の定義を使います。すなわち、投影したい点とSP(今回は側面図なのでSPv)を直線で結び、PPとの交点を求めます。少々難解ですが放射線と集中線のスライドも参照してください。
陰影は透視図法の中でも特に難易度が高く、上記の作図法も基礎から全部押さえていかないと、頭がついていかないと思います。そのあたりは数学と同じで、前の学年で習得したことを次の学年で使ったりするので、途中でつまずくと、以降は全然分からなくなります。
ただ裏を返せば、1つ分かると芋づる式に全部分かったりするので、その瞬間を迎えられれば、すごく幸せになります。
球のパースについて
パースフリークスの方でいくつかご質問をいただきましたので、こちらで詳細を回答させていただきます。
Q1.球にパースはかかりますか?
透視図法では正対している平面でもない限りパースがかからないということはなく、よって球にもパースがかかります。 パースフリークスでは球のページで解説していますが、球の輪郭線は透視図上で
- 円
- 楕円
- 放物線
- 双曲線
のいずれかになります。これらの図形はいずれも円錐曲線と呼ばれるもので、円錐のどこかを切断したときに出来る断面の形状になります。
放物線や双曲線はちょっと分かり難いと思いますが、これらの曲線になるケースというのは画面に球全体が入りきらない場合に限られます。逆に言うと球の全体がすっぽり収まる場合は、円または楕円にしかなりません。
Q2.現実世界で球を見ると、(楕円には見えず)常に正円に見えませんか?
こういう疑問を持つことは重要です。多分答えはYESでしょう。なぜなら、現実世界で球を見るとき、球は視界の中心(付近)にいるはずなので。
人間の目というのは実は非常に視野が狭く、物体がくっきり見える範囲はわずか2°程度しかないと言われています。よってなにかをしっかり見ようとすると、必ず視界の中心に置かないといけないんですね。もちろん中心以外にあるものも見えますが、円とか楕円とかが分かるレベルではないと思います。
さらに言うと、脳の解釈としてはパースがかかった図形ではなく、もとの形状で把握しようとするので、円とか楕円とかではなく、球体は球体に見えると表現した方が適切かもしれません。机の上に長方形の紙を置いたとして、多分その紙はパース的には台形に見えてるはずですが、人間の脳は本来の形である長方形として認識してしまいます。なので肉眼で見てどう見える(感じる)かと、絵としてどう描くかは切り離して考えた方がいいかもしれません。
この質問の回答にはならないのですが、パースフリークスでは「画角」-「自然な画とは」の「透視図上における変形の解釈」というカラムで、球をなぜ円錐曲線として描くのかということについて説明しています。(言葉足らずな解説なので、異論が出るかもしれませんが)
Q3.相当な広角でない限りは、球の輪郭は正円で描いてしまって問題ないでしょうか?
これは私も描いてみないと分からない問題だったので、実際に作画してみました。(足線法で描いています)
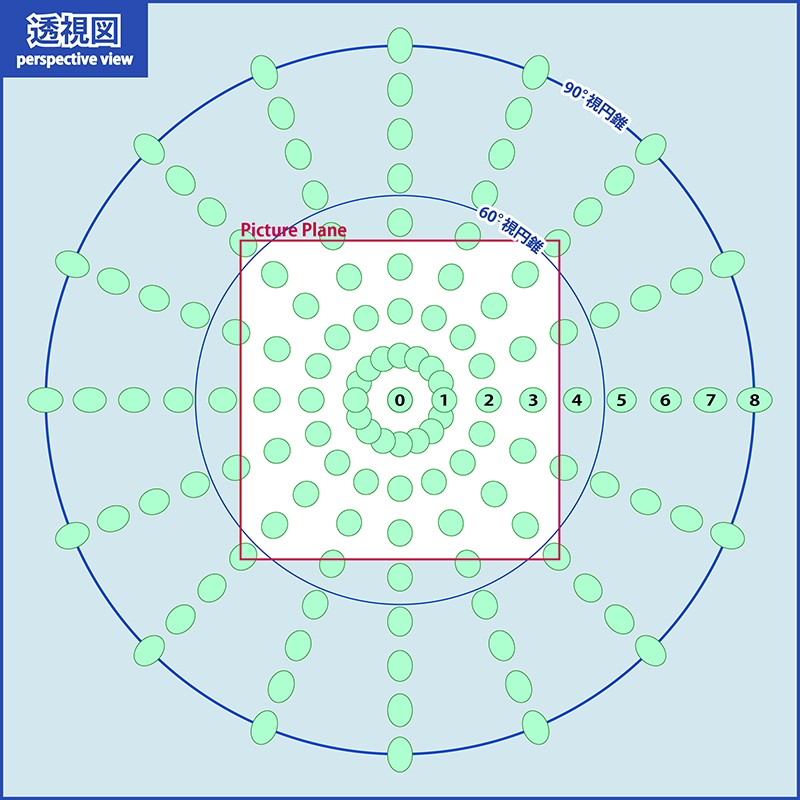
ご指摘いただいた通り、標準的な画角(60°以内程度)では、ほとんど正円という結果になりました。といっても、60°付近では扁平率は10%ぐらいはあるので、完全な円として描くより、気持ち楕円にした方が良さそうではあります。
画角に対する楕円の偏平率をまとめてみました。あくまでも今回描いた円の大きさに対するものなので、一般にこの値というわけではありませんが。
| No. | 扁平率 (%) | 画角 (deg) |
|---|---|---|
| 0 | 0.00 | 0.0 |
| 1 | 0.77 | 14.3 |
| 2 | 3.01 | 28.1 |
| 3 | 6.45 | 41.1 |
| 4 | 10.58 | 53.1 |
| 5 | 15.22 | 64.0 |
| 6 | 20.00 | 73.7 |
| 7 | 24.76 | 82.4 |
| 8 | 29.30 | 90.0 |
もう1点、別の方から影のパースに関するご質問をいただいていますので、また後日回答させていただきます。(8月5日)
さらに1件、8月26日にも頂いていたようです。ご質問いただいた量が多いですが、今月は多分時間が取れると思うので、ぼちぼち回答していきます。
透視図法における直方体の見える面の数
透視図法で絵を描いておられる方であれば、経験則的に次のような性質があることを知っておられると思います。
- 1点透視の直方体は、1~3つの面が見える。
- 2点透視の直方体は、2~3つの面が見える。
- 3点透視の直方体は、3つの面が見える。
※以下の説明では立方体の図を使いますが、直方体であっても性質は変わりません。
| 1点透視 | 2点透視 | 3点透視 |
|---|---|---|
 |
 |
 |
これらの法則は多くの場合は正しく当てはまるのですが、厳密に言えば間違いであり、本当は「1~3点透視のいずれであっても、見える面の数は1~3のいずれの場合もありうる」が正解です。すなわち、見える面の数と何点透視であるかは本質的には関係がありません。
具体例を見ていきましょう。下の左図は2点透視図ですが、右中央のサイコロは1面しか見えていません。同様に真ん中の図は3点透視図にも関わらず、右上のサイコロは1面しか見えず、その他の上段と右列のサイコロは2面しか見えません。右図はやはり3点透視図ですが、上段のサイコロが2面しか見えていません。
|
2点透視 (1点透視に近い) |
3点透視 (1点透視に近い) |
3点透視 (2点透視に近い) |
|---|---|---|
|
|
|
|
すでに表ヘッダに書かれている通り、これらの図は2点透視や3点透視と言いながらも、1点透視や2点透視に近い視線の向きで物体を描いたものです。
つまり実際が何点透視であっても、1点透視に近い向きで物体を見れば1面しか見えないパターンは存在し、2点透視に近い向きで物体を見れば2面しか見えないパターンが存在することを示しています。このような性質があるため、冒頭で挙げた法則はあながち的外れとも言えないのです。
ここで少し深く考えてみましょう。そもそも、なぜ面が見えたり見えなかったりするのでしょうか? (以下の説明を理解するには、透視図法の基礎知識が必要です。詳細はパースフリークスをご覧ください)
1.一点透視の場合
まずは1点透視図を使って考えていきましょう。下図をご覧ください。(外周部のサイコロは歪みが大きいですが、説明の都合で広角の図を使っているだけですので、気にしないでください)
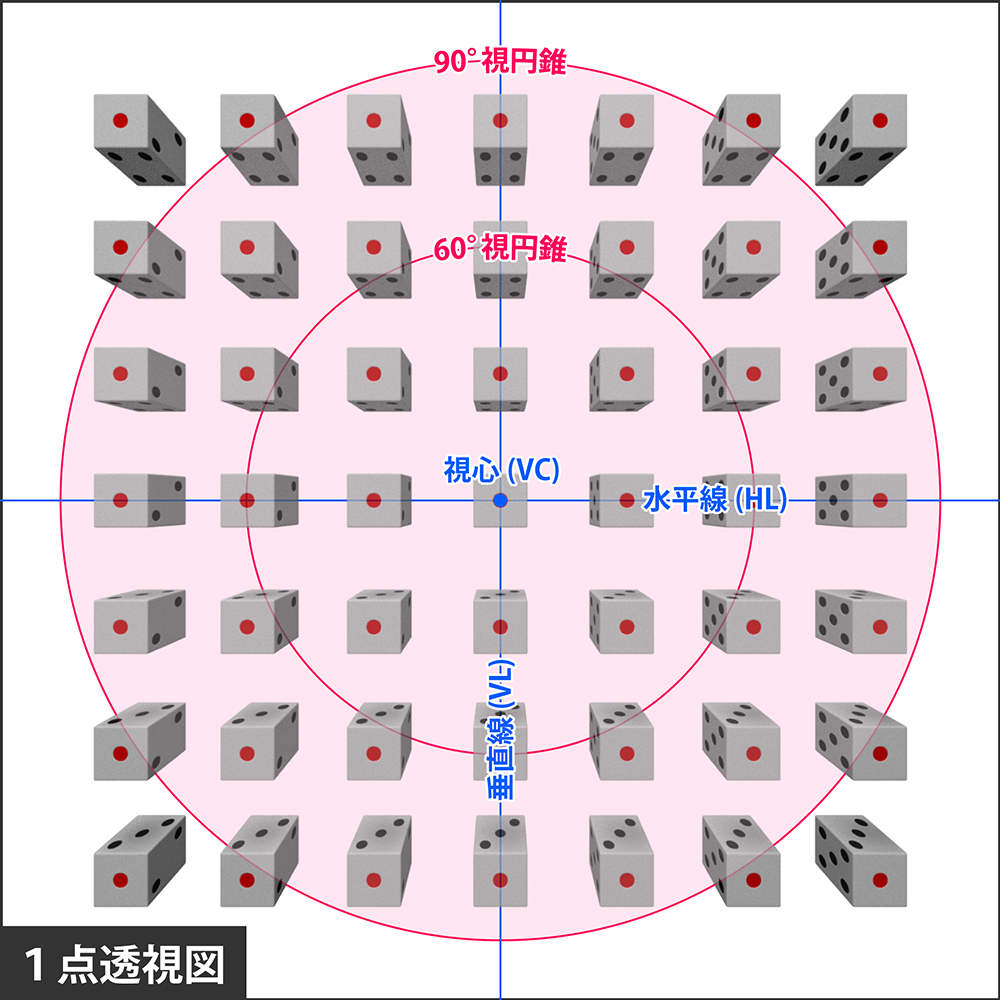
サイコロの置かれている位置によって、見える面が異なることが確認できます。
例えば、立方体の上面である3の目は水平線より下にある場合のみ見え、下面(4の目)は、水平線より上にある場合のみ見えます。
同様に右面(2の目)は垂直線の左側で、左面(5の目)は垂直線の右側でのみ見えることが確認できますね。
どうやら、どの面が見えるかは消失線(水平線や垂直線の総称)がカギを握っていそうです。
では、消失線上のサイコロについてはどうでしょうか? 水平線上のサイコロはすべて上面と下面のいずれもが見えないことが確認できます。また垂直線上のサイコロは左面と右面が共に見えません。
そして、両方の線上に位置する中央のサイコロに至っては、上下左右いずれの面も見えず、正面の1の目だけが見える状態になっています。
以上のことから、次の性質が浮かび上がります。
また、ここから次の法則が導き出されます。
- 水平線を跨ぐように配置される直方体は、上下面が見えない。
- 垂直線を跨ぐように配置される直方体は、左右面が見えない。
- 消失点を覆うように配置される直方体は、上下左右面が見えない。
法則3については、消失点が2本の消失線の交点であるという性質から導くことができます。
ある程度、法則がまとまってきましたが、上下左右などという表現は曖昧ですので、もう少し一般的な表現に置き換えてみます。
- 消失線を跨ぐように配置される直方体は、その消失線に収束する面が見えない。
- 消失点を覆うように配置される直方体は、その消失点に収束する辺を持つ面が見えない。
これで一般形になりました。法則2は法則1を二重に満たした場合にすぎませんので、基本的には法則1だけを覚えておけば良いことになります。
最終的に見える面の数は、以下の法則を満たします。
- 2本の消失線を跨ぐ(=消失点を覆う)ように配置される直方体は、面が1つしか見えない。
- 1本の消失線を跨ぐように配置される直方体は、面が2つしか見えない。
- 消失線を跨がないように配置される直方体は、面が3つ見える。
2.二点透視の場合
ここまでは1点透視図を使って説明してきましたが、実は2点透視図や3点透視図であっても、この法則は成り立ちます。
まずは2点透視図の例を見てみましょう。

2点透視図は3本の消失線HL,VL1,VL2を持ちます。
HLを跨ぐ場合に上下の面が見えなくなる性質は1点透視図と同様ですが、垂直線に相当する消失線は左右2本に分かれ、それぞれを跨ぐサイコロは、それぞれの消失線に収束する面が見えていないことが確認できます。
また、消失線のどちら側にいるかで見える面が異なることも確認できます。具体的にはVL1の左側では6の目が見え、右側では1の目が見えます。またVL2の左側では2の目が、右側では5の目が見えることが確認できます。
ここで注意しなければならないのは、上図が説明のための広角図であるという点です。実際の絵を描く際は、基本的に適正画角の範囲内(目安60°視円錐の内側)が作画領域になりますので、左右の消失線を跨ぐことはなく、常に1と2の目だけが見えることになります。
しかし、もう1点注意すべきは、観測者の視線の向きを示す角度パラメータです。(私の描く図では習慣的に「左○°右○°」のような表記を使用しています)
上図は90°視円錐の縁に2つの消失点が乗る形、すなわちサイコロを斜め45°から見るような視線の向きを取っていますが、これを斜め15°ぐらいの浅い角度にするとどうなるでしょうか?
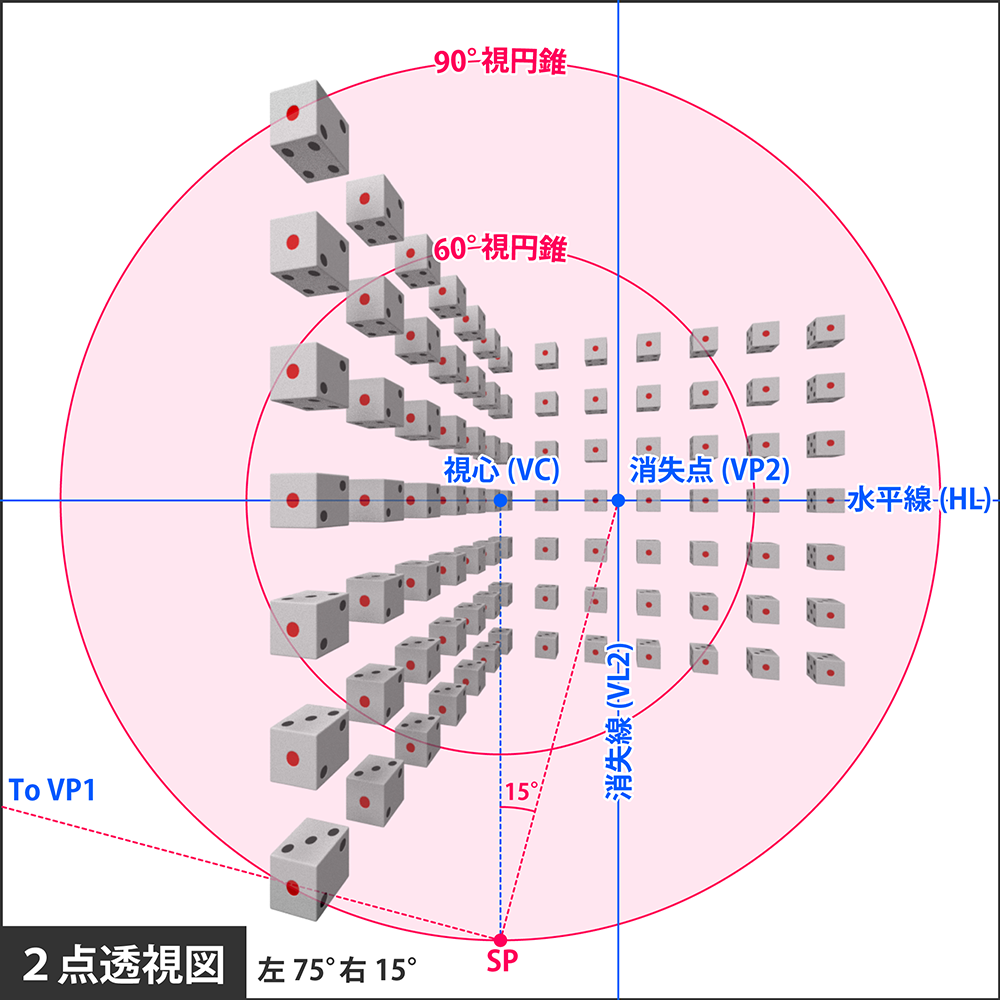
結果はこのようになり、消失点VP1が遙か遠くに行ってしまう代わりに、VP2は視心に接近します。すると消失線VL2が適正画角内に入ることになり、これを跨ぐサイコロも現れうることになります。
このような現象が起こるのは、角度が浅いとき、すなわち1点透視に近い視線の向きである場合に限られます。
よって1点透視に近い構図であれば、消失点の付近で面がほぼ1つしか見えない現象が発生することになります。
(図中で15°となっている角度が0°になった場合が1点透視図です)
3.三点透視の場合
作図線が密集して見づらいですが、下図を使って説明していきます。
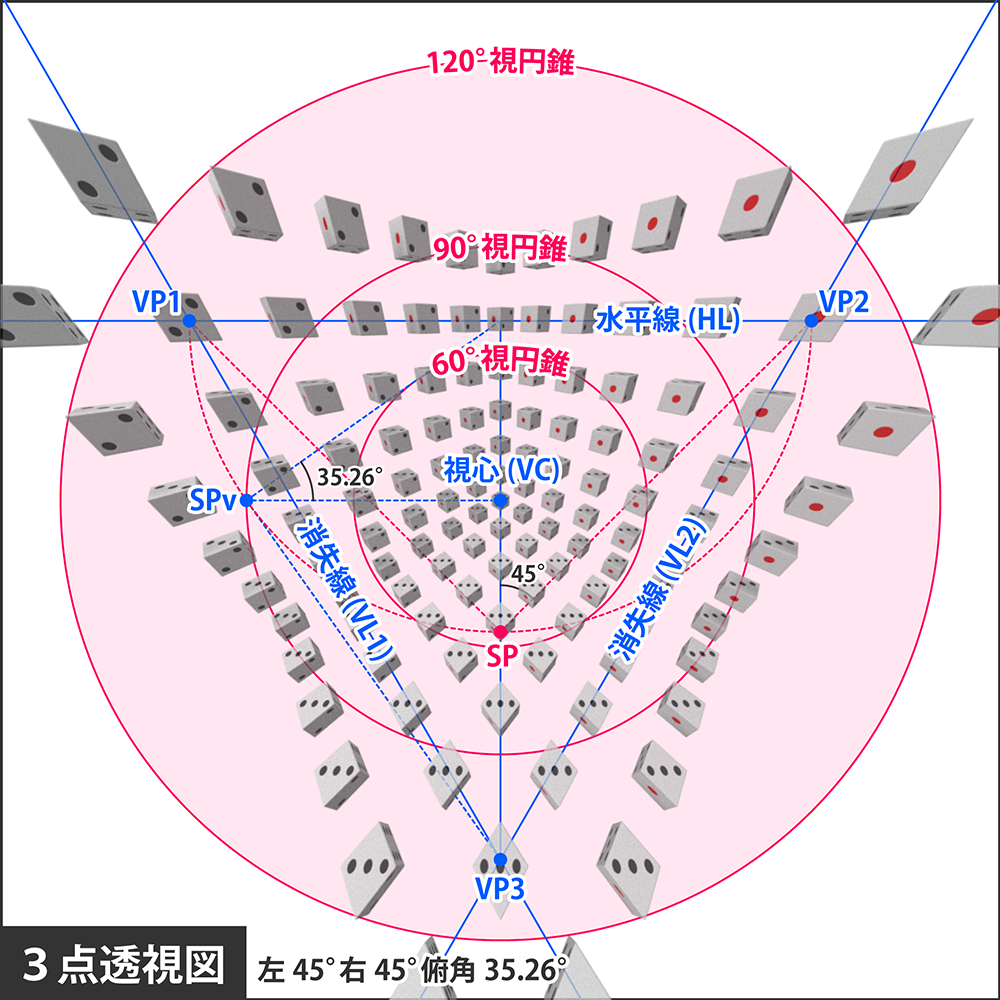
3点透視図には3本の消失線HL, VL1, VL2が存在しますが、これらを跨ぐように位置するサイコロは、面が2つしか見えていないことが確認できます。さらに3つの消失点VP1, VP2, VP3上に乗るサイコロは面が1つしか見えません。
見える面が変化する境界はやはり消失線となっています。3の目が見えるのは水平線の下側だけですし、4の目が見えるのは水平線の上側だけです。
VL1の左側では6の目が見え、右側では1の目が見えます。さらにVL2の左側は2の目が見え、右側になると5の目が見えます。
上図もまた広角図ですので、60°視円錐の内側だけに絞れば、1~3の目しか見えません。適正画角内では消失線を跨がないため、見える面が変化しないのです。
もちろん、角度パラメータを変え、2点透視や1点透視に近い視線の向きを取れば、適正画角内でも面が1~2個しか見えないという現象は発生します。
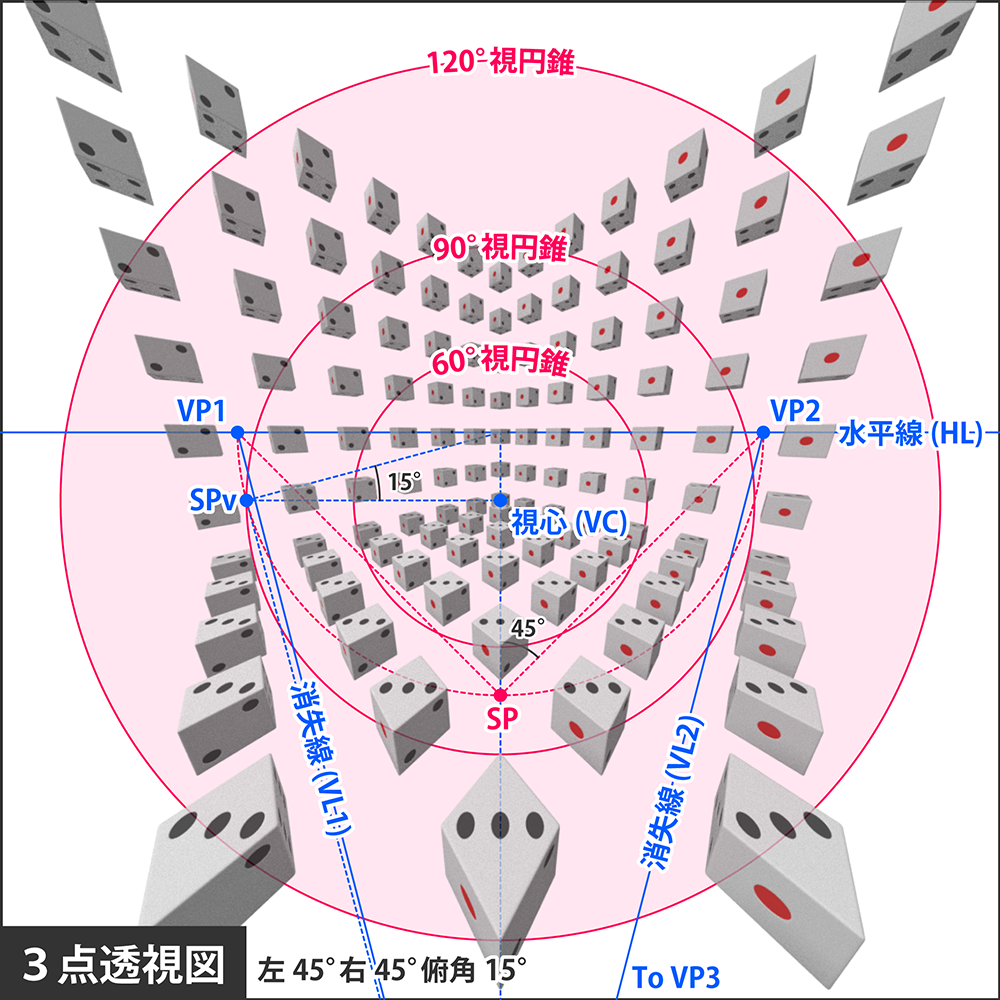
左図は左右の角度をそのままに俯角のみを15°に変更したものです。見下ろす角度が浅くなったため、水平線が視心に接近し、2点透視図とあまり変わらない見た目になりました。
このような構図では、適正画角内であっても、面が2つしか見えないパターンが発生します。
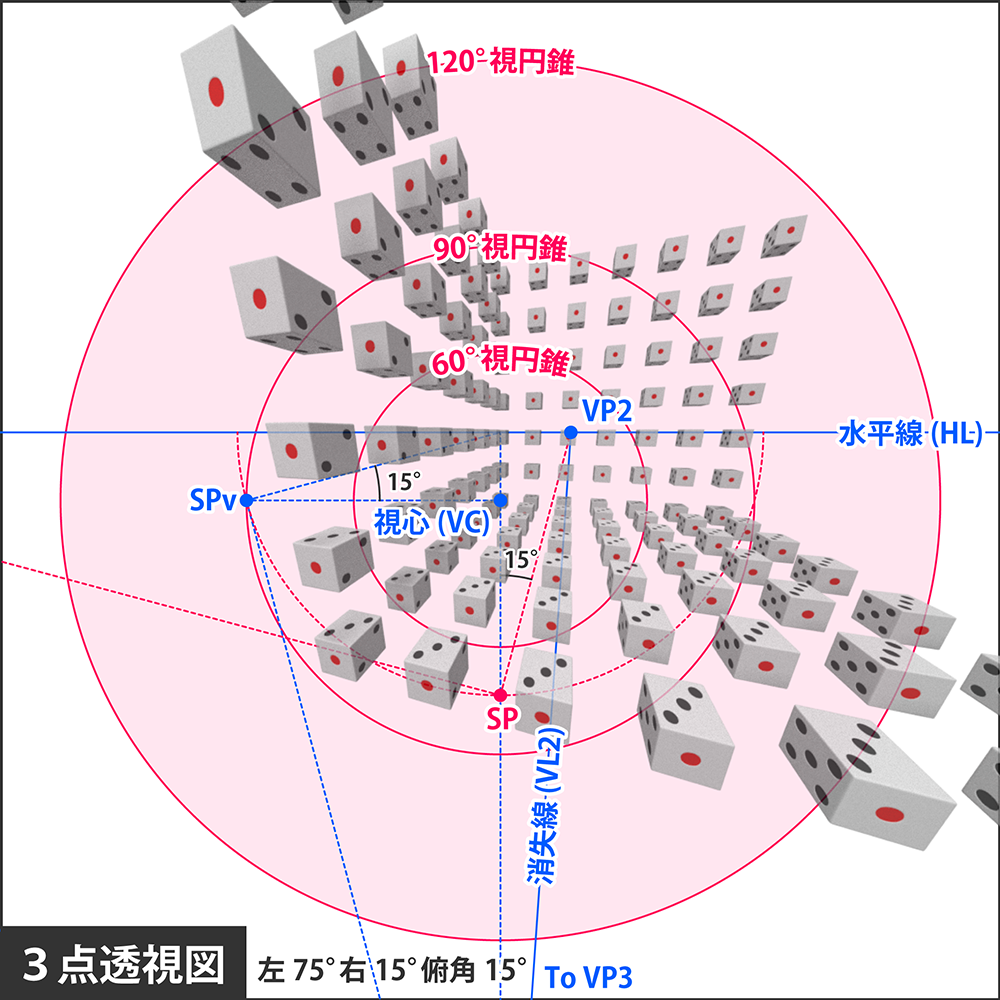
さらに左右の角度も浅くなると、左図のようになります。
ここまで来ると、パッと見の印象は1点透視図とほぼ変わらないでしょう。事実、消失点の1つであるVP2が視心のすぐ近くに現れています。角度を浅くすればするほど、消失点と視心は接近し、完全に0°にしてしまえば、消失点と視心が一致する本物の1点透視図になります。
改めて図を観察すると、やはり消失線HLやVL2上に乗るサイコロは2面しか見えず、消失点VP2の位置にあるサイコロは1面しか見えないことが確認できます。
以上、1~3点透視のそれぞれにおいて、直方体の見える面がどのように変化するかを見てきましたが、結論として何点透視であっても「直方体が消失線上にある場合は、その消失線に収束する2つの面が共に見えず、そうでない場合はいずれか1つの面が見える。どちらの面が見えるかは消失線のどちら側に位置しているかで決まる」という性質があることが分かりました。
次回は、1点透視や2点透視において、正面を向いたまま床や天井が見える現象について、詳しく説明したいと思います。(本エントリはパースフリークスQ&Aの回答として作成しました)


