透視図法における直方体の見える面の数
透視図法で絵を描いておられる方であれば、経験則的に次のような性質があることを知っておられると思います。
- 1点透視の直方体は、1~3つの面が見える。
- 2点透視の直方体は、2~3つの面が見える。
- 3点透視の直方体は、3つの面が見える。
※以下の説明では立方体の図を使いますが、直方体であっても性質は変わりません。
| 1点透視 | 2点透視 | 3点透視 |
|---|---|---|
 |
 |
 |
これらの法則は多くの場合は正しく当てはまるのですが、厳密に言えば間違いであり、本当は「1~3点透視のいずれであっても、見える面の数は1~3のいずれの場合もありうる」が正解です。すなわち、見える面の数と何点透視であるかは本質的には関係がありません。
具体例を見ていきましょう。下の左図は2点透視図ですが、右中央のサイコロは1面しか見えていません。同様に真ん中の図は3点透視図にも関わらず、右上のサイコロは1面しか見えず、その他の上段と右列のサイコロは2面しか見えません。右図はやはり3点透視図ですが、上段のサイコロが2面しか見えていません。
|
2点透視 (1点透視に近い) |
3点透視 (1点透視に近い) |
3点透視 (2点透視に近い) |
|---|---|---|
|
|
|
|
すでに表ヘッダに書かれている通り、これらの図は2点透視や3点透視と言いながらも、1点透視や2点透視に近い視線の向きで物体を描いたものです。
つまり実際が何点透視であっても、1点透視に近い向きで物体を見れば1面しか見えないパターンは存在し、2点透視に近い向きで物体を見れば2面しか見えないパターンが存在することを示しています。このような性質があるため、冒頭で挙げた法則はあながち的外れとも言えないのです。
ここで少し深く考えてみましょう。そもそも、なぜ面が見えたり見えなかったりするのでしょうか? (以下の説明を理解するには、透視図法の基礎知識が必要です。詳細はパースフリークスをご覧ください)
1.一点透視の場合
まずは1点透視図を使って考えていきましょう。下図をご覧ください。(外周部のサイコロは歪みが大きいですが、説明の都合で広角の図を使っているだけですので、気にしないでください)
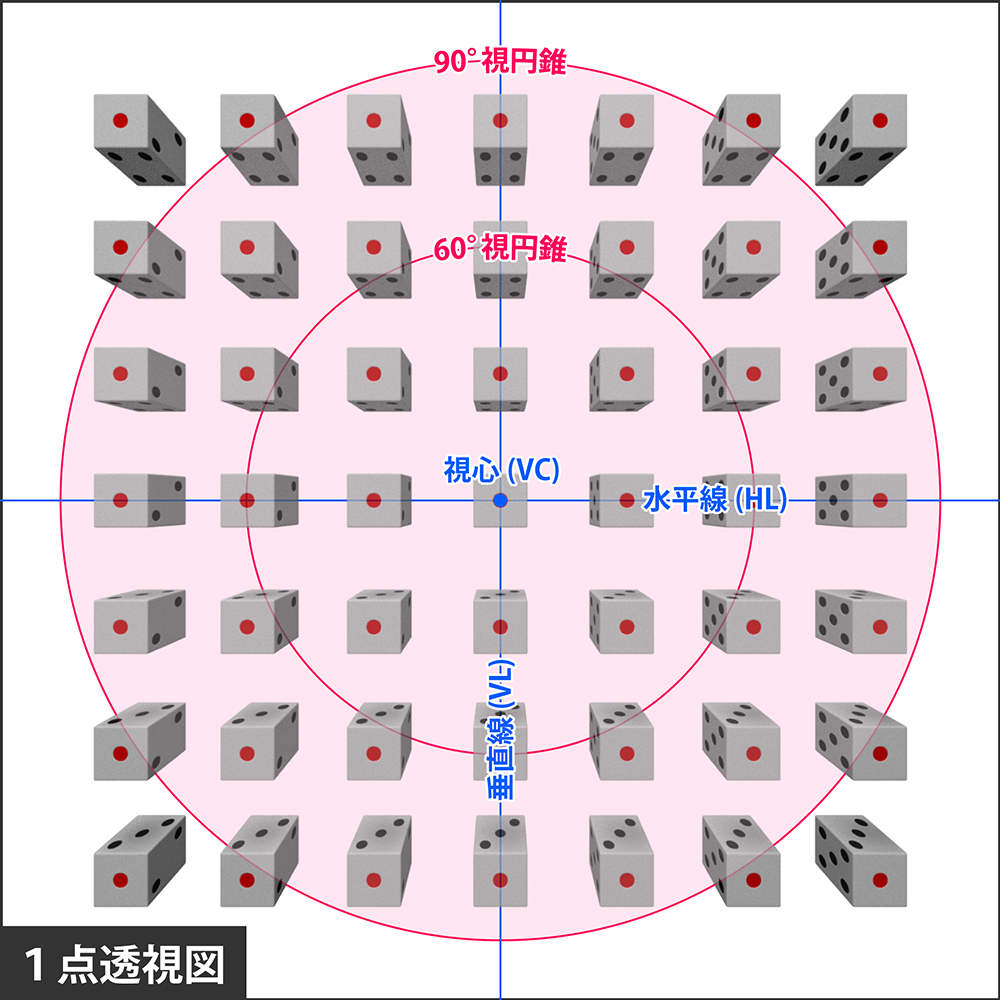
サイコロの置かれている位置によって、見える面が異なることが確認できます。
例えば、立方体の上面である3の目は水平線より下にある場合のみ見え、下面(4の目)は、水平線より上にある場合のみ見えます。
同様に右面(2の目)は垂直線の左側で、左面(5の目)は垂直線の右側でのみ見えることが確認できますね。
どうやら、どの面が見えるかは消失線(水平線や垂直線の総称)がカギを握っていそうです。
では、消失線上のサイコロについてはどうでしょうか? 水平線上のサイコロはすべて上面と下面のいずれもが見えないことが確認できます。また垂直線上のサイコロは左面と右面が共に見えません。
そして、両方の線上に位置する中央のサイコロに至っては、上下左右いずれの面も見えず、正面の1の目だけが見える状態になっています。
以上のことから、次の性質が浮かび上がります。
また、ここから次の法則が導き出されます。
- 水平線を跨ぐように配置される直方体は、上下面が見えない。
- 垂直線を跨ぐように配置される直方体は、左右面が見えない。
- 消失点を覆うように配置される直方体は、上下左右面が見えない。
法則3については、消失点が2本の消失線の交点であるという性質から導くことができます。
ある程度、法則がまとまってきましたが、上下左右などという表現は曖昧ですので、もう少し一般的な表現に置き換えてみます。
- 消失線を跨ぐように配置される直方体は、その消失線に収束する面が見えない。
- 消失点を覆うように配置される直方体は、その消失点に収束する辺を持つ面が見えない。
これで一般形になりました。法則2は法則1を二重に満たした場合にすぎませんので、基本的には法則1だけを覚えておけば良いことになります。
最終的に見える面の数は、以下の法則を満たします。
- 2本の消失線を跨ぐ(=消失点を覆う)ように配置される直方体は、面が1つしか見えない。
- 1本の消失線を跨ぐように配置される直方体は、面が2つしか見えない。
- 消失線を跨がないように配置される直方体は、面が3つ見える。
2.二点透視の場合
ここまでは1点透視図を使って説明してきましたが、実は2点透視図や3点透視図であっても、この法則は成り立ちます。
まずは2点透視図の例を見てみましょう。

2点透視図は3本の消失線HL,VL1,VL2を持ちます。
HLを跨ぐ場合に上下の面が見えなくなる性質は1点透視図と同様ですが、垂直線に相当する消失線は左右2本に分かれ、それぞれを跨ぐサイコロは、それぞれの消失線に収束する面が見えていないことが確認できます。
また、消失線のどちら側にいるかで見える面が異なることも確認できます。具体的にはVL1の左側では6の目が見え、右側では1の目が見えます。またVL2の左側では2の目が、右側では5の目が見えることが確認できます。
ここで注意しなければならないのは、上図が説明のための広角図であるという点です。実際の絵を描く際は、基本的に適正画角の範囲内(目安60°視円錐の内側)が作画領域になりますので、左右の消失線を跨ぐことはなく、常に1と2の目だけが見えることになります。
しかし、もう1点注意すべきは、観測者の視線の向きを示す角度パラメータです。(私の描く図では習慣的に「左○°右○°」のような表記を使用しています)
上図は90°視円錐の縁に2つの消失点が乗る形、すなわちサイコロを斜め45°から見るような視線の向きを取っていますが、これを斜め15°ぐらいの浅い角度にするとどうなるでしょうか?
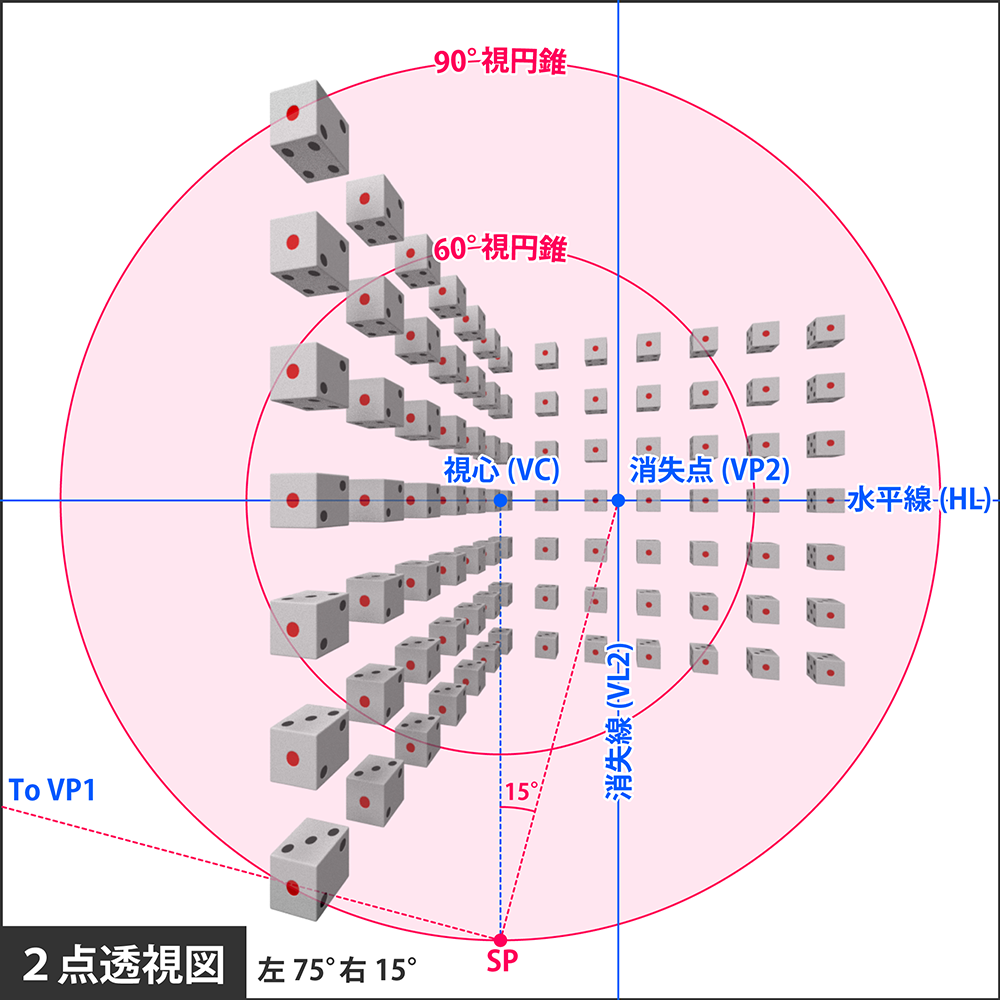
結果はこのようになり、消失点VP1が遙か遠くに行ってしまう代わりに、VP2は視心に接近します。すると消失線VL2が適正画角内に入ることになり、これを跨ぐサイコロも現れうることになります。
このような現象が起こるのは、角度が浅いとき、すなわち1点透視に近い視線の向きである場合に限られます。
よって1点透視に近い構図であれば、消失点の付近で面がほぼ1つしか見えない現象が発生することになります。
(図中で15°となっている角度が0°になった場合が1点透視図です)
3.三点透視の場合
作図線が密集して見づらいですが、下図を使って説明していきます。
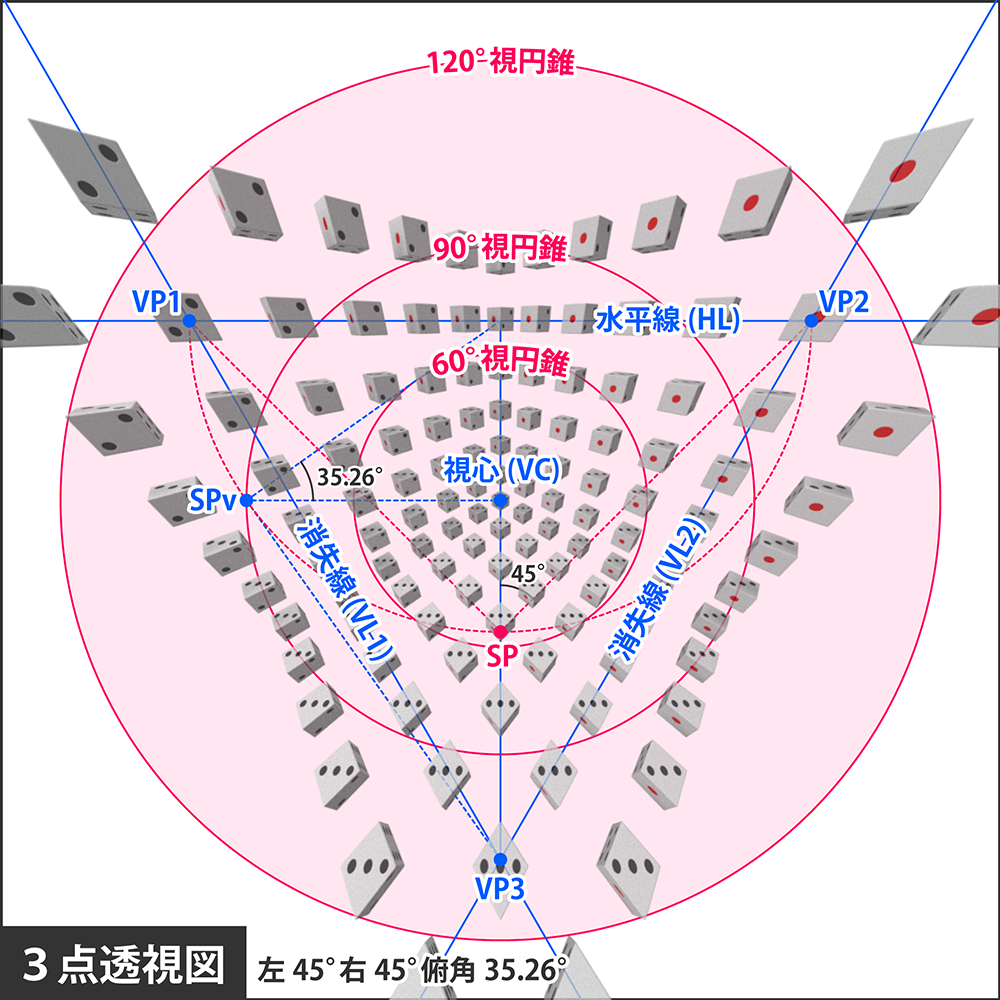
3点透視図には3本の消失線HL, VL1, VL2が存在しますが、これらを跨ぐように位置するサイコロは、面が2つしか見えていないことが確認できます。さらに3つの消失点VP1, VP2, VP3上に乗るサイコロは面が1つしか見えません。
見える面が変化する境界はやはり消失線となっています。3の目が見えるのは水平線の下側だけですし、4の目が見えるのは水平線の上側だけです。
VL1の左側では6の目が見え、右側では1の目が見えます。さらにVL2の左側は2の目が見え、右側になると5の目が見えます。
上図もまた広角図ですので、60°視円錐の内側だけに絞れば、1~3の目しか見えません。適正画角内では消失線を跨がないため、見える面が変化しないのです。
もちろん、角度パラメータを変え、2点透視や1点透視に近い視線の向きを取れば、適正画角内でも面が1~2個しか見えないという現象は発生します。
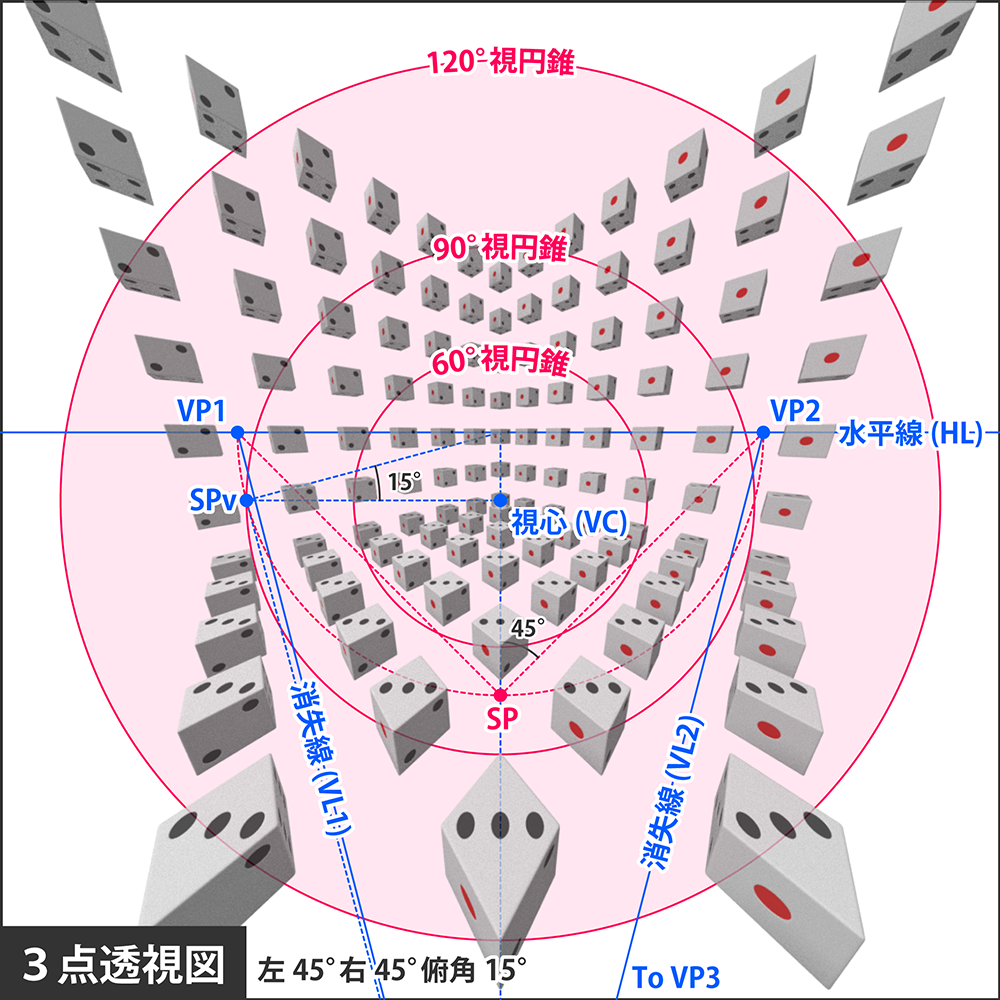
左図は左右の角度をそのままに俯角のみを15°に変更したものです。見下ろす角度が浅くなったため、水平線が視心に接近し、2点透視図とあまり変わらない見た目になりました。
このような構図では、適正画角内であっても、面が2つしか見えないパターンが発生します。
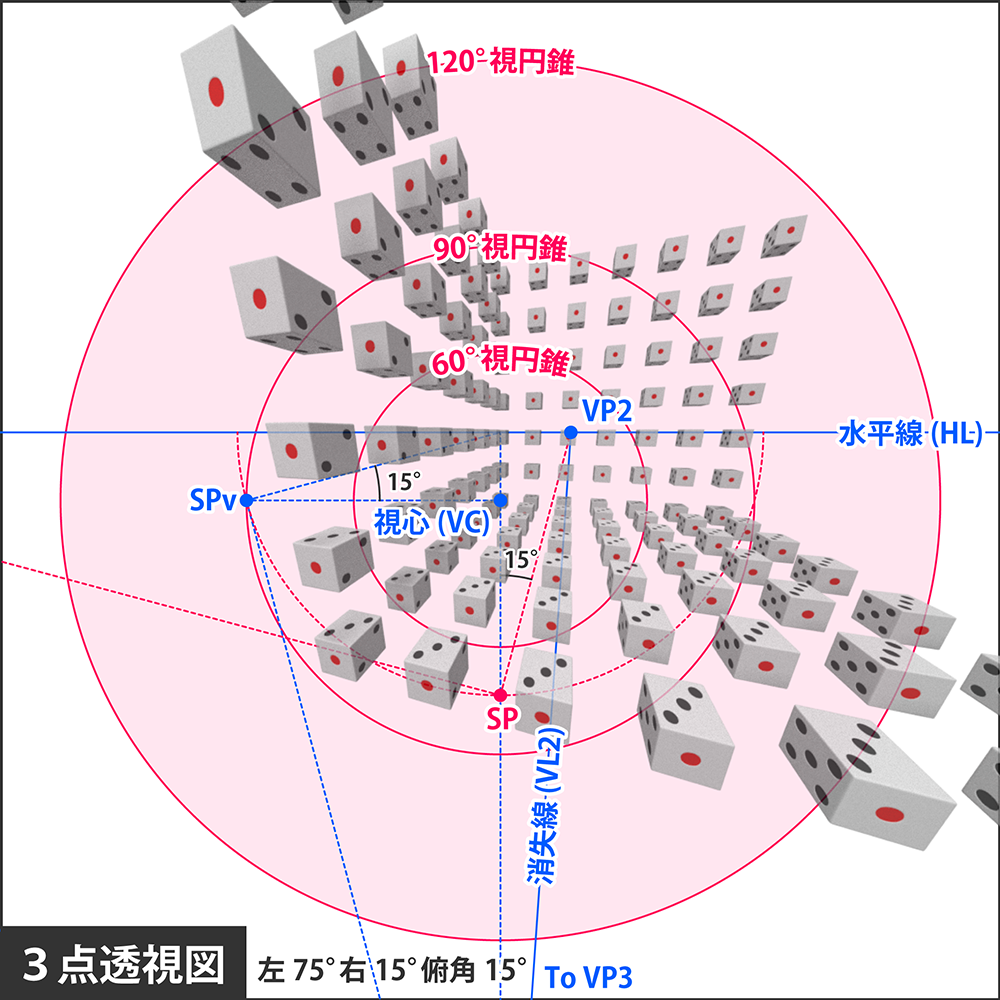
さらに左右の角度も浅くなると、左図のようになります。
ここまで来ると、パッと見の印象は1点透視図とほぼ変わらないでしょう。事実、消失点の1つであるVP2が視心のすぐ近くに現れています。角度を浅くすればするほど、消失点と視心は接近し、完全に0°にしてしまえば、消失点と視心が一致する本物の1点透視図になります。
改めて図を観察すると、やはり消失線HLやVL2上に乗るサイコロは2面しか見えず、消失点VP2の位置にあるサイコロは1面しか見えないことが確認できます。
以上、1~3点透視のそれぞれにおいて、直方体の見える面がどのように変化するかを見てきましたが、結論として何点透視であっても「直方体が消失線上にある場合は、その消失線に収束する2つの面が共に見えず、そうでない場合はいずれか1つの面が見える。どちらの面が見えるかは消失線のどちら側に位置しているかで決まる」という性質があることが分かりました。
次回は、1点透視や2点透視において、正面を向いたまま床や天井が見える現象について、詳しく説明したいと思います。(本エントリはパースフリークスQ&Aの回答として作成しました)


